PEER Advanced Field School 2023

class: center, middle, inverse, title-slide

.title[
# PEER Advanced Field School 2023
]
.subtitle[
## Day 2 - Individuals in Networks
]
.author[
### Eric Brewe <br> Professor of Physics at Drexel University <br>
]
.date[
### 15 June 2023, last update: 2023-06-19
]

---

# Welcome Back!

### Our project is about building and analyzing the Workshop network

# Let's load our data

This workshop assumes you did the work from day 1 and you know how to install libraries, read csv files into data, and to manipulate data in R.

The benefit of having done the work previously is that we don't have to re-do it (unless we want to change something)

So I took the network at the end of workshop #1 and saved it as a .rds file. I could have saved it as a pair of csv files and rebuilt the network, but if I save as rds it will be ready to go!

To load an rds file the syntax is a little different:

```r
gr <- readRDS(here("data", "WokshopNetwork.rds"))
```

---
# Let's inspect our data

```r
gr
```

```
## # A tbl_graph: 60 nodes and 101 edges
## #
## # A directed multigraph with 8 components
## #
## # A tibble: 60 × 4
##   name  AMPM            Dessert                   Pages
##   <chr> <chr>           <chr>                     <dbl>
## 1 5106  morning person. Brownies                    350
## 2 6633  morning person. I don't care for dessert.    12
## 3 7599  night owl.      Ice Cream                   300
## 4 4425  morning person. I don't care for dessert.     0
## 5 2495  morning person. Brownies                    264
## 6 6355  night owl.      Ice Cream                     4
## # ℹ 54 more rows
## #
## # A tibble: 101 × 2
##    from    to
##   <int> <int>
## 1     1     1
## 2     2    35
## 3     3    14
## # ℹ 98 more rows
```

---
# Let's plot it quickly

.pull-left[
## Which node is the most important?

````

```r
gr %>%
  ggraph(layout = "kk") +
  geom_edge_link() +
  geom_node_point(aes(color = Dessert)) +
  theme(legend.position="bottom")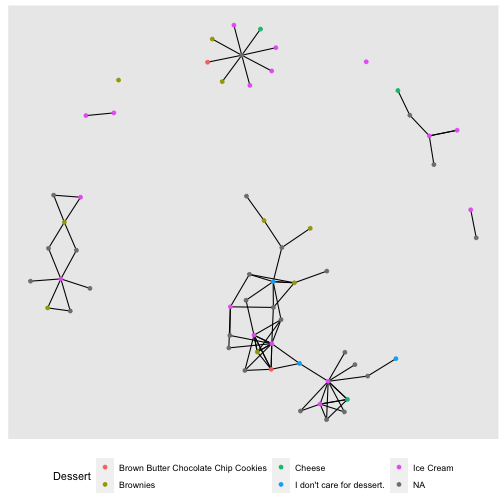
```
````

]

.pull-right[
![](PEER_Individuals_Networks_files/figure-html/plotGrR-1.png)
]
---
# Let's explore centrality

### One view of importance is how many people you are connected to.
- **Degree** = number of edges a node is involved in.
- **In Degree** = number of incoming edges
- **Out Degree** = number of outgoing edges

Lets calculate degree

```r
gr %>%
  activate(nodes) %>%
  mutate(deg = centrality_degree(mode = "total")) %>%
  arrange(desc(deg)) -> gr
  
gr
```

```
## # A tbl_graph: 60 nodes and 101 edges
## #
## # A directed multigraph with 8 components
## #
## # A tibble: 60 × 5
##   name  AMPM            Dessert                   Pages   deg
##   <chr> <chr>           <chr>                     <dbl> <dbl>
## 1 7743  morning person. Ice Cream                   300    14
## 2 2921  morning person. Ice Cream                   426    12
## 3 1386  night owl.      Ice Cream                   500    11
## 4 7040  morning person. I don't care for dessert.   400     9
## 5 9929  morning person. Brownies                    527     8
## 6 5051  night owl.      Ice Cream                   240     8
## # ℹ 54 more rows
## #
## # A tibble: 101 × 2
##    from    to
##   <int> <int>
## 1    28    28
## 2    43    32
## 3    29    10
## # ℹ 98 more rows
```

---
# Let's use the degree in a plot

.pull-left[
````

```r
gr %>%
  ggraph(layout = "kk") +
  geom_edge_link() +
  geom_node_point(aes(size = deg )) +
  theme(legend.position="bottom")
```
````

]

.pull-right[
![](PEER_Individuals_Networks_files/figure-html/plotGrCentR-1.png)
]
---
# Let's see about just In-degree

```r
gr %>%
  activate(nodes) %>%
  mutate(InDeg = centrality_degree(mode = "in")) %>%
  arrange(desc(InDeg)) -> gr
  
gr
```

```
## # A tbl_graph: 60 nodes and 101 edges
## #
## # A directed multigraph with 8 components
## #
## # A tibble: 60 × 6
##   name  AMPM            Dessert   Pages   deg InDeg
##   <chr> <chr>           <chr>     <dbl> <dbl> <dbl>
## 1 5844  <NA>            <NA>         NA     8     8
## 2 7743  morning person. Ice Cream   300    14     5
## 3 1386  night owl.      Ice Cream   500    11     4
## 4 2169  <NA>            <NA>         NA     4     4
## 5 4755  <NA>            <NA>         NA     4     4
## 6 9929  morning person. Brownies    527     8     3
## # ℹ 54 more rows
## #
## # A tibble: 101 × 2
##    from    to
##   <int> <int>
## 1    38    38
## 2    51    20
## 3    39    15
## # ℹ 98 more rows
```

---
# Let's use in degree in our plot

.pull-left[
````

```r
gr %>%
  ggraph(layout = "kk") +
  geom_edge_link() +
  geom_node_point(aes(size = InDeg )) +
  theme(legend.position="bottom")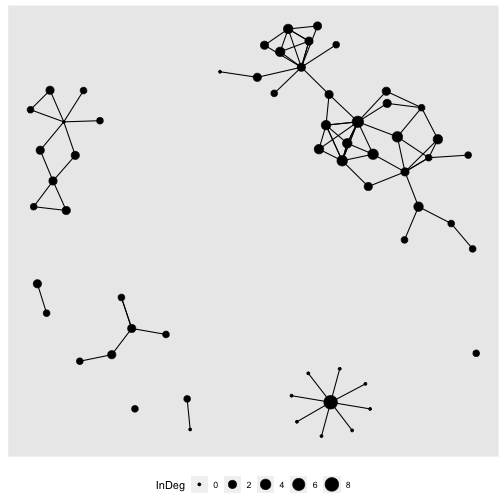
```
````

]

.pull-right[
![](PEER_Individuals_Networks_files/figure-html/plotGrInCentR-1.png)
]

---
# Let's compare centrality plots.

### You might have noticed, the plots change layouts

.pull-left[

#### To address this we set a layout...

````

```r
GrLayout = create_layout(gr, 
                layout = "kk")

ggraph(GrLayout) +
  geom_edge_link() +
  geom_node_point(aes(size = InDeg)) +
  theme(legend.position="bottom")
```
````

]

.pull-right[

#### The only issue is, we then can't change nodes/attributes.

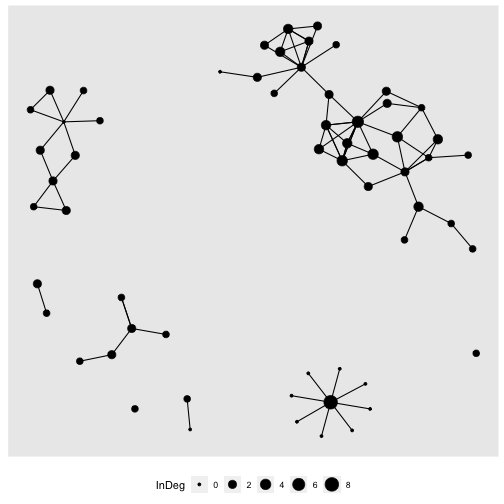
![](PEER_Individuals_Networks_files/figure-html/TestLayout-1.png)

]
---
# Let's compare in-degree and out-degree

.pull-left[

```r
ggraph(GrLayout) +
  geom_edge_link() +
  geom_node_point(aes(size = InDeg)) +
  theme(legend.position="bottom")
```

![](PEER_Individuals_Networks_files/figure-html/InDegLayout-1.png)
]

.pull-right[

```r
ggraph(GrLayout) +
  geom_edge_link() +
  geom_node_point(aes(size = deg)) +
  theme(legend.position="bottom")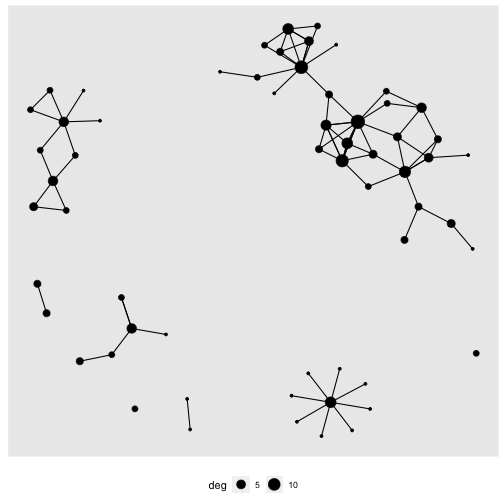
```

![](PEER_Individuals_Networks_files/figure-html/OutDegLayout-1.png)

]
---
# Let's explore some other centrality measures

### Here is a list of all of the centrality measures that you have access to in tidygraph:

### https://tidygraph.data-imaginist.com/reference/centrality.html

## This is a workshop and thus far I've done most of the work!  It is your turn!

1. As a group, choose one of the centrality measures from the list.
2. Calculate the centrality measure, use it in the plotting recipe we've been using, and be ready to describe what you think this centrality metric measures. 
3. You will have 10-15 minutes.  
4. Be ready to present - talk about what the centrality measure is and the properties that the centrality measure emphasizes.

---
# Let's use centrality in hypothesis testing

We should establish a research question. How about:

### Are morning people or night owls more central in our network?

To test this we might use:
1. An independent samples t-test to see if the means of a centrality metric is different.
2. A linear model to explore the relationships between the grouping variable and the outcome variable.

Either way, we need to choose a centrality metric.

.center[.font170[Our winner...centrality_eigen!]]

---
# Let's first calculate and plot eigenvector centrality

Eigenvector centrality is interesting because it allows a node to inherit centrality from neighbors. It works with weighted networks, and but it treats directed networks as undirected.

We want to calculate eigenvector centrality, then add it as an attribute to our graph, and add it to our layout dataframe.

```r
gr %>%
  activate(nodes) %>%
  mutate(CentE = centrality_eigen()) %>%
  arrange(desc(CentE)) -> gr

#This makes a dataframe of names and CentE
gr %>%
  activate(nodes) %>%
  select(name, CentE) %>%
  as_tibble()-> CentEdf

#This adds it to the GrLayout dataframe.
GrLayout = left_join(GrLayout, CentEdf, by = "name")
```

---
# Let's plot with eigenvector centrality

.pull-left[
````

```r
ggraph(GrLayout) +
  geom_edge_link() +
  geom_node_point(aes(size = CentE)) +
  theme(legend.position="bottom")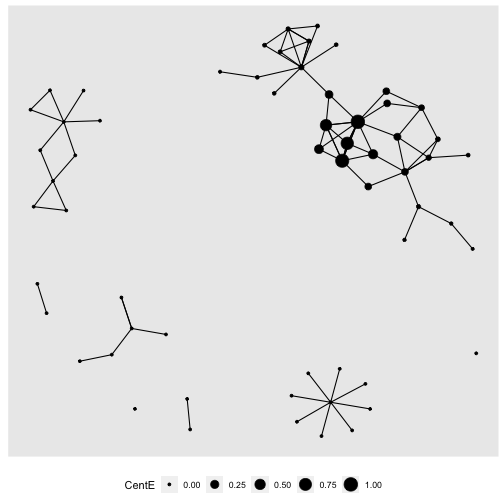
```
````
]

.pull-right[

![](PEER_Individuals_Networks_files/figure-html/PlotECentR-1.png)

]
.center[
### Cool, different nodes are important!
]
---
# Let's get ready to use in linear model

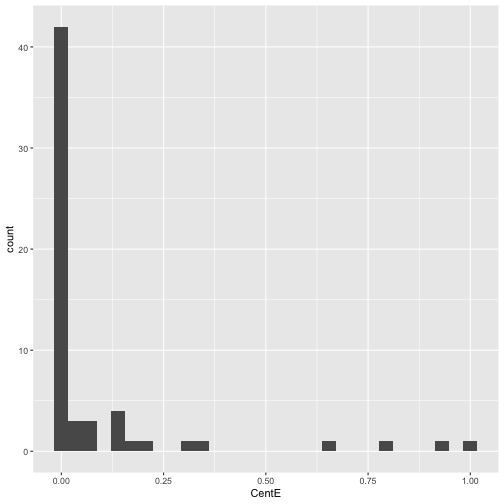
### First, let's see how it is distributed

.pull-left[
````

```r
gr %>%
  select(AMPM,CentE) %>%
  as_tibble() %>%
  ggplot(., aes(x = CentE)) + 
  geom_histogram()
```
````

]

.pull-right[

### Not Normal!
![](PEER_Individuals_Networks_files/figure-html/BoxPlotR-1.png)
]

---
# Let's reflect

### Remember when I said...

"Nodes and interactions are interdependent*"

and

"\* Violates basic assumption of inferential statistics"

Well, this is the problem, because network metrics are interdependent, they are invariably not normally distributed. Which means we have to take some additional precautions about how we use them in hypothesis testing. Which means...
--

.center.font190[Bootstrapping!]

.footnote[
I said it here: https://ericbrewe.com/slides/peer_network_school_2023/peer_network_theory#5
]

---
# Let's get ready to bootstrap

### What is bootstrapping?
Bootstrapping is a resampling method, where you draw samples based on your existing dataset, calculate your measure of interest, store this, and then rinse and repeat.

.center.font170[R has a package for that.]

--
### Let's install the package "boot" and load it.

````

```r
install.packages("boot")
library(boot)
```
````

---
# Let's set up a bootstrapped model

### Our goal was to answer the question, "Are morning people or night owls more central in our network?"

So we will run a bootstrapped linear model to look at this relationship.

First, get our data and assign it to its own dataframe (you don't have to, but.)

```r
GrLayout %>%
  select(AMPM,CentE) -> LmData
```

Next, we need to define the linear model as a function. Why? I'll explain in next slide.

```r
bs <- function(formula, data, indices) {
  d <- data[indices,]
  fit <- lm(formula, data = d)
  return(coef(fit))
}
```

---
# Let's run this linear model

### Finally, we use the boot command to call the function
Since we want to run this once, and keep our results around, we should do two things.

1. Set our seed so that we can replicate if need be.
2. Assign our results to a data structure.

```r
set.seed(327)

results <- boot(data = LmData, 
*    statistic = bs,
     R = 50, 
     formula = CentE ~ AMPM)
```

---
# Let's explore the results

.pull-left[

### First, what is the result if we don't use bootstrapping?

```r
lm(CentE ~ AMPM, data = LmData)
```

```
## 
## Call:
## lm(formula = CentE ~ AMPM, data = LmData)
## 
## Coefficients:
##    (Intercept)  AMPMnight owl.  
##       0.119801       -0.007688
```
]
.pull-right[
### Now, what about the bootstrap?

```r
results
```

```
## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = LmData, statistic = bs, R = 50, formula = CentE ~ 
##     AMPM)
## 
## 
## Bootstrap Statistics :
##         original       bias    std. error
## t1*  0.119801337  0.009599055  0.05622172
## t2* -0.007688342 -0.018954699  0.07718224
```

```r
boot.ci(results, type = "basic")
```

```
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 50 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = results, type = "basic")
## 
## Intervals : 
## Level      Basic         
## 95%   (-0.0314,  0.2197 )  
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable
```

]

---
#Let's figure out what this means

- Original is the estimate without resampling.
- Bias is the difference between the bootstrap mean and the original.
- t1* is the intercept
- t2* is the coefficient for the AMPM variable

The confidence interval on the coefficients are (-0.0314, 0.2197)

### So, are morning people more central than night owls?

.center.font200[Probabaly not

😞
]