R For SNA

class: center, middle, inverse, title-slide

# R For SNA
## Workshop 3
### Eric Brewe <br> Associate Professor of Physics at Drexel University <br>
### 18 August 2020, last update: 2020-08-18

---

# Welcome Back!

### Our project is about building and analyzing the Workshop network

So we will **not** need a new project folder, we will continue to use RForSNA, which you should have set up in WS1.

This time we will add a new .Rmd file, give it a title like "network_properties.Rmd"

So navigate to your RForSNA file and create a new .Rmd file.

Then, add a code chunk to load the libraries necessary and run this chunk.

```r
library(tidyverse) #tools for cleaning data 
library(igraph)  #package for doing network analysis
library(tidygraph) #tools for doing tidy networks
library(here) #tools for project-based workflow
library(ggraph) #plotting tools for networks
library(boot)  #to do resampling
```

---
# Let's load our data

This workshop assumes you did the work from week 1 and you know how to install libraries, read csv files into data, and to manipulate data in R.

The benefit of having done the work previously is that we don't have to re-do it (unless we want to change something)

So I took the network at the end of workshop #1 and saved it as a .rds file. I could have saved it as a pair of csv files and rebuilt the network, but if I save as rds it will be ready to go!

To load an rds file the syntax is a little different:

```r
gr <- readRDS(here("data", "WorkshopNetwork.rds"))
```

---
# Let's plot it quickly

While we are at it we might as well set a layout.

.pull-left[
## Whare are distinctive features of the network?

````

```r
GrLayout <- create_layout(gr,
                          layout = "kk")

ggraph(GrLayout) +
  geom_edge_link() +
  geom_node_point() +
  theme(legend.position="bottom")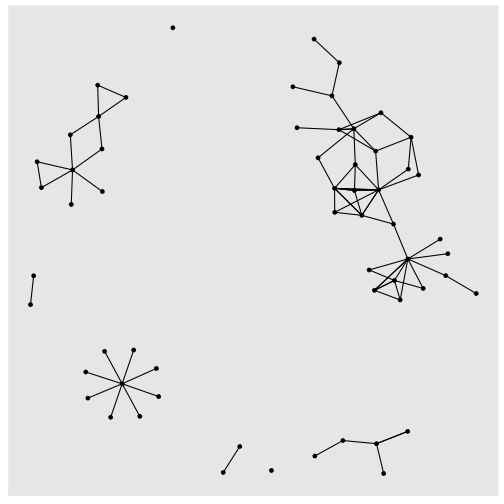
```
````

]

.pull-right[
![](RForSNA_WS3_files/figure-html/plotGrR-1.png)
]
---
# Let's explore whole network metrics

**These are fairly easy to calculate**
- Density: Proportion of possible connections that exist
- Diameter: Longest Shortest Path across network
- Reciprocity: Extent to which each directed edge is a two way edge
- Transitivity: Extent to which three connected nodes form triangles
- Average Path Length: Average shortest distance between every pair of nodes

**These require a bit more work**
- Giant: Number of nodes connected to largest component
- Homophily: Extent to which nodes with similar attribute are connected
- Average degree: This is pretty descriptive.

This is a list of many common graph metrics used in tidygraph
https://rdrr.io/cran/tidygraph/man/graph_measures.html

---
# Lets calculate a couple of these...

### For many of these it is a very simple one line command.
Here is density

```r
edge_density(gr)
```

```
## [1] 0.02853107
```

Here is diameter, note that with tidygraph you have to use the with_graph() function, and specify the graph and function graph_diameter()

```r
with_graph(gr, graph_diameter())
```

```
## [1] 6
```

--
.center.font200[So?]

---
# Let's calculate a couple of others

###  It is your turn, choose one of the ones that are easy to calculate and make the calculation.

```r
with_graph(gr, graph_reciprocity()) #Reciprocity
```

```
## [1] 0.2142857
```

```r
transitivity(gr) #Transitivity
```

```
## [1] 0.2669492
```

```r
with_graph(gr, graph_mean_dist()) #Average Distance
```

```
## [1] 1.88125
```

---
# Let's create a function

### Creating a function accomplishes two things:
1. We can calculate some of the harder to calcluate metrics
2. We do not have to re-do each time we want to analyze a new network.

```r
GrFunction <- function(gr){
  Giant = max(clusters(gr)$csize)
  AMPMHomophily = with_graph(gr, graph_assortativity(AMPM))
  DessertHomophily = with_graph(gr, graph_assortativity(Dessert))
  AveDeg = gr %>%
    activate(nodes) %>%
    mutate(Deg = centrality_degree( mode = 'total') ) %>%
    select(Deg) %>%
    as_tibble() %>%
    summarise(AveDeg = mean(Deg))
  df = tibble(Giant, AMPMHomophily, DessertHomophily, AveDeg )
  return(df)
}
```

---
# Let's run this function

```r
GrFunction(gr)
```

```
## # A tibble: 1 x 4
##   Giant AMPMHomophily DessertHomophily AveDeg
##   <dbl>         <dbl>            <dbl>  <dbl>
## 1    30        -0.723           0.0468   3.37
```

### What do these numbers mean?
--

*Giant* = 30, there are 30 people connected in the largest component.

*AMPM Homophily*, Since this is negative, there is a propensity for people to associate with others, (e.g., A morning person is more likely connected to a night owl)

*Dessert Homophily*, this is pretty close to zero, so there doesn't seem to be an association.

*AveDeg*, the average person has 3.37 incoming or outgoing edges

### Is this unique?

---
# Let's decide if our network is unique

### What is the big problem with the network that we have collected?

1. We have one network.
2. There is no variance in the metrics.  
3. What is the null hypothesis/model?

---
# Let's talk about camps

### This is a place where there are sort of two camps of network analysis

.pull-left[
### Statistical Camp

- **Variance:** Permutation/resampling techniques such as bootstrap. 
- **Null hypothesis:** Exponential random graph models (ERGMs) Or rewired network

]

.pull-right[
### Graph Theoretic Camp

- **Null Model** Theory driven models
    - Random Graph (Erdos-Renyi)
    - Small World (Watts-Strogatz)
    - Preferential Attachment (Barabasi-Albert)
- **Variance** Network simulation
]

---
# Let's try a graph-theoretic model

### We'll generate a Erdos-Renyi model and compare our graph characteristics

First, we need to tell the simulation how many nodes and edges to include.

```r
N_Nodes = with_graph(gr, graph_order())
N_Edges = with_graph(gr, graph_size())
```
--

### Now we can actually generate the graph

```r
set.seed(522)
ER_gr <- play_erdos_renyi(n = N_Nodes, m = N_Edges)
```

---
# Let's check out our ER Graph

.pull-left[

```r
ER_gr %>%
  ggraph(layout = "kk") + 
  geom_edge_link() +
  geom_node_point() +
  theme(legend.position="bottom")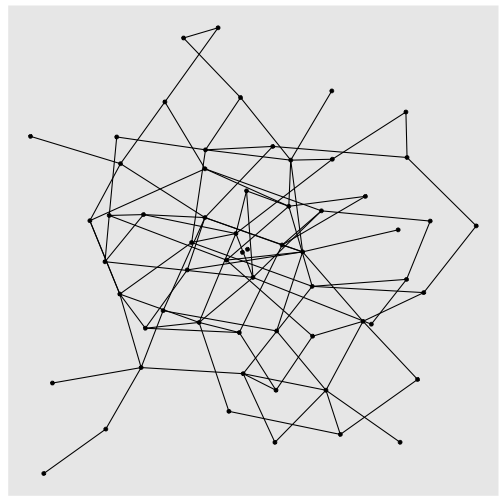
```

]

.pull-right[
![](RForSNA_WS3_files/figure-html/plotERT-1.png)
]

---
# Let's put them side by side

.pull-left[

```r
ggraph(GrLayout) +
  geom_edge_link() +
  geom_node_point()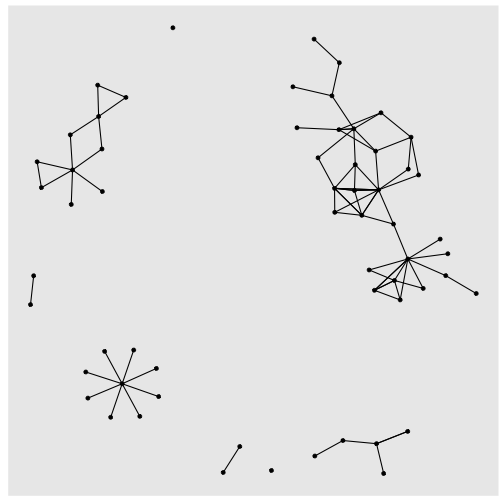 
```

![](RForSNA_WS3_files/figure-html/plotWSNet-1.png)

]
.pull-right[

```r
ER_gr %>%
  ggraph(layout = "kk") + 
  geom_edge_link() +
  geom_node_point()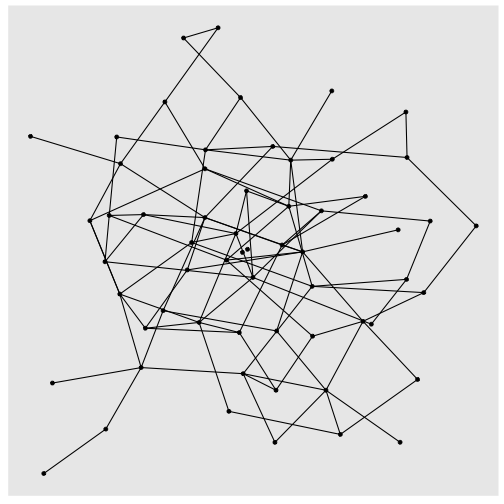 
```

![](RForSNA_WS3_files/figure-html/plotERT2-1.png)
]

---
# Let's assign attributes

### In order to compare homophily, we need our ER_gr to have the same attributes.

I emailed you all an additional file that has a random graph with attributes (because it was a pain to add those in.) So now, we need to add these in...

```r
ER_gr_attr <- readRDS(here("data", "RandomGraph.rds")) 
```

```
## # A tbl_graph: 58 nodes and 101 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 58 x 3 (active)
##   name  AMPM            Dessert                  
##   <chr> <chr>           <chr>                    
## 1 5106  morning person. Brownies                 
## 2 6633  morning person. I don't care for dessert.
## 3 7599  night owl.      Ice Cream                
## 4 4425  morning person. I don't care for dessert.
## 5 2495  morning person. Brownies                 
## 6 6355  night owl.      Ice Cream                
## # … with 52 more rows
## #
## # Edge Data: 101 x 2
##    from    to
##   <int> <int>
## 1     1    12
## 2     1    25
## 3     1    33
## # … with 98 more rows
```

---
# Let's use our function to compare

### Measured network

```r
GrFunction(gr)
```

```
## # A tibble: 1 x 4
##   Giant AMPMHomophily DessertHomophily AveDeg
##   <dbl>         <dbl>            <dbl>  <dbl>
## 1    30        -0.723           0.0468   3.37
```

### Random network

```r
GrFunction(ER_gr_attr) 
```

```
## # A tibble: 1 x 4
##   Giant AMPMHomophily DessertHomophily AveDeg
##   <dbl>         <dbl>            <dbl>  <dbl>
## 1    58        -0.684         -0.00420   3.48
```

---
# Let's now do this 100 times!

In order to do this, lets reduce the number of graph metrics we want to calculate.

```r
SmGrFunction <- function(gr){
  Giant = max(clusters(gr)$csize)
  Recip  = with_graph(gr, graph_reciprocity())
  Trans = transitivity(gr) 
  Dist = with_graph(gr, graph_mean_dist()) 
  Dia = with_graph(gr, graph_diameter())
  df = tibble(Giant, Recip, Trans, Dist, Dia )
  return(df)
}
```

```r
for (i in 1:100)
  {
  test_gr = play_erdos_renyi(n = N_Nodes, m = N_Edges)
  if(i==1) 
    {df <- SmGrFunction(test_gr)} else
    {df <- bind_rows(df, SmGrFunction(test_gr))}
  }
```

---
# Let's explore our simulated networks

```r
head(df)
```

```
## # A tibble: 6 x 5
##   Giant  Recip  Trans  Dist   Dia
##   <dbl>  <dbl>  <dbl> <dbl> <dbl>
## 1    56 0.0396 0.0561  5.14    14
## 2    58 0.0198 0.0464  6.43    23
## 3    55 0.0396 0.0636  5.04    12
## 4    60 0.0198 0.135   4.87    10
## 5    59 0.0594 0.0677  5.41    16
## 6    57 0      0.0752  4.69    14
```
---
# Let's get a summary
And lets average these out.

```r
df %>%
  summarise(across(everything(), mean)) 
```

```
## # A tibble: 1 x 5
##   Giant  Recip  Trans  Dist   Dia
##   <dbl>  <dbl>  <dbl> <dbl> <dbl>
## 1  58.0 0.0297 0.0545  5.16  13.7
```

And standard deviations.

```r
df %>%
  summarise(across(everything(), sd))
```

```
## # A tibble: 1 x 5
##   Giant  Recip  Trans  Dist   Dia
##   <dbl>  <dbl>  <dbl> <dbl> <dbl>
## 1  1.46 0.0230 0.0239 0.602  2.49
```

---
# Let's compare with measured

```r
df %>%
  summarise(across(everything(), mean)) 
```

```
## # A tibble: 1 x 5
##   Giant  Recip  Trans  Dist   Dia
##   <dbl>  <dbl>  <dbl> <dbl> <dbl>
## 1  58.0 0.0297 0.0545  5.16  13.7
```

```r
SmGrFunction(gr)
```

```
## # A tibble: 1 x 5
##   Giant Recip Trans  Dist   Dia
##   <dbl> <dbl> <dbl> <dbl> <dbl>
## 1    30 0.214 0.267  1.88     6
```

---
# Let's get a confidcence interval

### If we want to estimate the confidence with which we think our measured network is different on one of these metrics, we can look for the percentiles.

Let's see if the measured average distance falls within the 95% of the simulated network....

```r
quantile(df$Dist, probs = c(0.025, 0.975))
```

```
##     2.5%    97.5% 
## 3.889960 6.243622
```

Since the measured average distance is outside of this range, we can say that the measured network is not a random network!

---
# Let's summarize

.font160[
1. We measured one network
2. To compare we generated a random network
3. We replicated 100 times
4. We checked whether metrics from the measured network falls within some confidence range.
5. We can say the measured network is different than random. 
]

---
# Let's reflect

.font120[

We did it!

1. We can import data into R
2. We can manipulate these data
3. We can create a network
4. We can plot a network
5. We can calculate a number of centrality measures
6. We can use these in plotting networks
7. We can use these in testing hypotheses
8. We can calculate a number of whole graph metrics
9. We can use these in comparing networks

]

---
# Let's note what we missed

.font150[

1. We didn't do community detection
2. We didn't really touch Base R
3. We didn't deal with ERGMs.
]

---
# Let's be thankful

.font200.center[
Thanks to Dali Ma

Thanks to SSRC

Thanks to all of you

👏
]